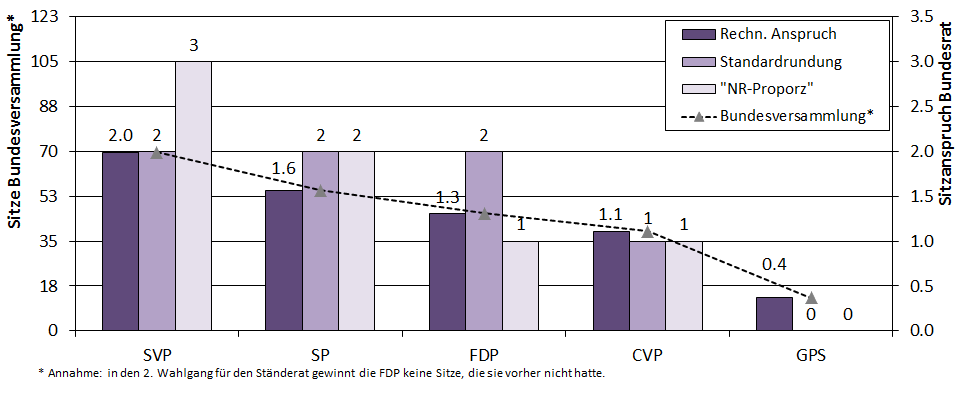
Denken wir den rechnerischen Anspruch der SVP auf zwei Bundesratssitze zu Ende, würden ihr am Ende sogar drei Sitze zustehen. Die FDP müsste einen Sitz abgeben. Letztlich sind aber politische Kriterien auch im in der Schweiz lange praktizierten Modell der Konkordanzdemokratie entscheidender für die Regierungsbildung als pseudo-mathematische Formeln.
Die veröffentlichte Meinung hat auf die Wahlen vom Wochenende reagiert. Die Ansicht, dass der Wählerwille einen zweiten SVP-Sitz gebietet, wird nunmehr nicht nur von der NZZ vertreten, sondern weit herum wiederholt. Das zugrundeliegende Argument ist, dass die grösste Partei gemäss ihrer Wählerstärke im Bundesrat vertreten sein sollte. Es greift also auf den Gedanken der spiegelbildlichen, proportionalen Vertretung der Parteien in der Regierung zurück.[1] Am lautesten kommt die Forderung von der FDP.
Wer nachrechnet, merkt schnell: würde die FDP der Forderung nach einem Bundesrat, der den Wählerwillen respektiert, nachleben, müsste sie der SVP ihren 2. Sitz zu Verfügung stellen.
Unklare Proportionalität: Wählerstärke oder Sitze in der Bundesversammlung?
Es gibt selbstverständlich keine Bundesratsformel, die mathematisch korrekt ist. Einzelne Länder sehen zwar solche Regierungszusammensetzungen verfassungsmässig vor [2], aber der schweizerische Bundesrat wird durch das Parlament nach dem Mehrheitsprinzip gewählt. Damit ist auch nicht klar, auf welcher Basis denn die Proportionalität, welche explizit oder implizit von Presse und FDP beschworen wird, beruhen soll. Entweder kann man die Wählerinnen und Wähler abbilden, oder dann das gewählte Parlament, wohl eher die Sitze in der Vereinigten Bundesversammlung als die Sitzverteilung im Nationalrat (siehe Tabelle 1).
Tabelle 1
Quelle: eigene Berechnungen
Abbildung 1 stellt ein Rechenbeispiel für die Vereinigte Bundesversammlung dar. (Bei allen Ständeratssitzen, die erst im zweiten Wahlgang besetzt werden, gehe ich davon aus, dass sie nicht die Partei wechseln.) Rechnen wir die 246 Sitze der Bundesversammlung auf Bundesratssitze um, dann entspricht ein Regierungsmandat (rechte Skala) ungefähr 35 Parlamentarierinnen und Parlamentariern (linke Skala). Der SVP stünden umgerechnet 2 Sitze zu, der SP 1.6, der FDP 1.3, der CVP 1.1. Den Grünen und den Kleinparteien fallen jeweils weniger als ein halbes Mandat zu. Sitzzuteilungsmethoden runden diese Sitzansprüche nun auf eine nahe gelegene ganze Zahl.
Sitzanspruch nach Sainte-Laguë
Die Sainte-Laguë-Formel, die auf der Standardrundung (kaufmännische Rundung) basiert, kommt in den kantonalen Wahlen in Basel-Stadt, aber auch in allen doppelt-proportionalen Wahlgesetzen zur Anwendung. Sie ergäbe jeweils zwei Sitze für die SVP, die SP, die FDP und einen Sitz für die CVP. Die FDP würde hier von einer grosszügigen Aufrundung profitieren. Grund dafür ist, dass bei einer strengen Standardrundung nur sechs Regierungssitze vergeben würden. In solchen Fällen wird der Divisor (also die Anzahl Sitze, die für ein Bundesratsmandat nötig sind), künstlich etwas gesenkt, und zwar solange, bis alle sieben Sitze vergeben sind (rechte Balken). Allerdings will ausgerechnet die FDP Schweiz in Wahlrechtsfragen von der Sainte-Laguë bislang nichts wissen, sie beharrt auf dem alten Nationalratsproporz, auch D’Hondt- oder Hagenbach-Bischoff genannt.
Sitzanspruch nach D’Hondt- oder Hagenbach-Bischoff
Das ist eine Formel, welche auf dem Abrundungsprinzip beruht: allen wird etwas genommen und an die Grossen zurückverteilt. Das macht für die Regierungsbildung auch Sinn, denn dort sollen die Kräfte gebündelt werden (und die Sainte-Laguë-Formel würde ungeliebte strategische Spiele ermöglichen). Demnach resultiert nach D’Hondt- oder Hagenbach-Bischoffeine Sitzverteilung von drei Sitzen für die SVP, zwei für die SP und je einen für die FDP und die CVP (mittlere Balken).
Das gleiche Spiel mit dem Taschenrechner resultiert, sobald wir auf die Wählerstärke oder die Sitzverteilung im Nationalrat abstellen, auch in einer 2–2‑1–1‑1-Formel, unter Einbezug der Grünen. 1959 gab es die Mehrdeutigkeit nicht, damals waren die Kräfteverhältnisse genügend klar und konsequent, um die 2–2‑2–1‑Formel zu legitimieren.
Keine Formel ist die sicher richtige
Für die Regierungsbildung sind die Formeln wenig sinnvoll. Es ist nicht klar, welche Berechnungsformel die richtige ist. In der öffentlichen Diskussion verwendet die Presse und verwenden die Parteien improvisierte, aber kurzlebige und inkonsequente Argumente: die Regeln zur Zusammensetzung des Bundesrates, die sie jeweils aus der historischen Zauberformel ableiten, gelten jeweils so lange, als es ihren politischen Zielen entspricht. Dann werden sie wieder neu definiert.
Zauberformel ist mehr als Mathematik
Die Zauberformel, die lange für den Bundesrat galt, war weniger eine Frage der mathematischen Proportionalität, als der Einbindung, des politischen Kompromisses, und der (freiwilligen) Zusammenarbeit. Historisch ist die Zauberformel unter anderem genau deswegen entstanden, weil die CVP verhindern wollte, dass die FDP im Bundesrat mit Schützenhilfe der SVP den Ton angab.[3]
Bundesversammlung wählt den Bundesrat
Richtig ist: die Bundesversammlung wählt den Bundesrat. Und da zählt auch der Ständerat mit, der vor allem in der neuen Legislatur anders aussieht als der Nationalrat. Ebenso wichtig wie die Proportionalität ist, dass der Bundesrat für seine Vorlagen Mehrheiten in beiden Kammern schaffen kann. Dies ist nur möglich mit Bundesratsparteien und Kandidaten, die Kompromisse eingehen und zur Zusammenarbeit — oder kurz: zur Konkordanz — bereit sind. Die Bundesversammlung entscheidet am 9. Dezember nach politischen Kriterien.
Referenzen
[1] Daniel Bochsler and Pascal Sciarini, “Neue Indikatoren Zur Bestimmung Der Arithmetischen Regierungskonkordanz ” Swiss Political Science Review 12, no. 1 (2006).
[2] Brendan O’Leary, Bernard Grofman, and Jørgen Elklit, “Divisor Methods for Sequential Portfolio Allocation in Multi-Party Executive Bodies: Evidence from Northern Ireland and Denmark,” American Journal of Political Science 49, no. 1 (2005).
[3] http://napoleonsnightmare.ch/2015/09/05/auftakt-zur-blutezeit-der-konkordanz/
Foto: EJPD